Jedenástka

Nie, nebojte sa. Nebudeme riešiť pravidlá týkajúce sa odpískania pokutového kopu za ruku alebo faul na hráča v šestnástke. Jedenástka sa vzťahuje na počet hráčov jedného mužstva na ihrisku v najrozšírenejšom variante futbalového zápasu 11 na 11.

Pri sledovaní špičkových futbalových mužstiev je často vidieť, že hráči sa na ihrisku dostávajú do priestorov, v ktorých by pri striktnom dodržiavaní svojich úloh zrejme nemali byť. Pravý obranca pri rýchlom protiútoku môže zbehnúť na miesto pravého krídla, stopér sa pri rohovom kope v šestnástke súpera postaví na miesto stredného útočníka, záložník zatiaľ zaujme miesto stopéra a tak ďalej. Z toho vyplynula jednoduchá, ale zaujímavá otázka. Koľkými spôsobmi je možné rozmiestniť jedenástku hráčov jedného mužstva na ihrisku?

Pomôžme si na začiatok športami, kde je omnoho menej hráčov ako jedenásť. Začnime napríklad tenisom a zápasom jednotlivcov. Jeden hráč A na ihrisku sa dá umiestniť len raz. V plážovom volejbale hrajú dvojice. Tie môžu byť umiestnené na ihrisku tak, že hráč A je vľavo a hráč B vpravo, alebo opačne. To sú dve možnosti: A – B alebo B – A. V trojkovom basketbale môžeme rozmiestnenie trojíc opísať takto: A – B – C, A – C – B, B – A – C, B – C – A, C – A – B, C – B – A. Dostávame spolu 6 trojíc. Skúste si spočítať, koľko štvoríc, teda umiestnení hráčov, by sme dostali v športovom odvetví – napríklad pri päťminútovom predĺžení v hokejom zápase, v ktorom hrajú 4 hráči (brankár a 3 hráči v poli) na oboch stranách.

Na vyriešenie otázky, ktorá sa týka rozmiestnenia 11 futbalových hráčov na ihrisku, môžeme použiť základný princíp kombinatoriky, ktorý sa zaoberá usporiadaním prvkov. Keďže ide o rozmiestnenie všetkých 11 hráčov, čo znamená, že každý hráč má svoje jedinečné miesto, použijeme permutáciu. Permutácia alebo poradie základného súboru n prvkov je skupina všetkých n prvkov, pri ktorej záleží na poradí prvkov v nej. Ako permutácia alebo premiestnenie sa označuje aj proces vytvorenia takejto skupiny. Slovo permutovať znamená obmieňať. Rozlišujeme permutácie s opakovaním a bez opakovania. Počet spôsobov, ako môžeme 11 hráčov rozmiestniť na ihrisku, je rovný počtu permutácií 11 prvkov (bez opakovania). Tento počet sa vypočíta ako 11! (11 faktoriál), čo môžeme napísať ako: 11! = 11 x 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1. No a po vynásobení všetkých členov dostaneme konečný výsledok 39 916 800 možností umiestnenia 11 hráčov jedného mužstva na ihrisku.

Uvedomme si teraz jednu vec. Každé mužstvo nastupuje na zápas v určitom rozostavení, napr. 4 – 3 – 3, 4 – 4 – 2, 3 – 4 – 3 a podobne. Má brankára, obrancov, strednopoliarov a útočníkov. Títo hráči majú na ihrisku svoje postavenie a na zápas ťažko nastúpi hráč hrávajúci na poste útočníka (Erling Halland) na post brankára (Ederson). Ako by sme teda dokázali vypočítať počet umiestnení hráčov na ihrisku v prípade rôznych rozostavení hráčov hrajúcich na svojim postoch?

Rozdelenie hráčov do skupín:

• Rozdeľme hráčov na brankára, obrancov, strednopoliarov a útočníkov podľa rozostavenia.
• Napríklad pre rozostavenie 4-4-2:
  • 1 brankár
  • 4 obrancovia
  • 4 stredopoliari
  • 2 útočníci

Výber hráčov pre jednotlivé pozície:

• Vyberieme hráča na pozíciu brankára.
• Vyberieme hráčov na pozície obrancov z zostávajúcich 10 hráčov.
• Vyberieme hráčov na pozície stredopoliarov zo zostávajúcich 6 hráčov.
• Vyberieme útočníkov z posledných 2 hráčov.

Výpočet počtu permutácií pre každú skupinu:

• Pre každú skupinu hráčov (obrancovia, stredopoliari, útočníci) vypočítame počet permutácií v rámci tejto skupiny.

Všeobecný vzorec:

• Ak máme k₁, k₂, …, k_m ​ hráčov na jednotlivých pozíciách (kde k₁ + k₂ +⋯+ k_m = 11), celkový počet možných usporiadaní je:

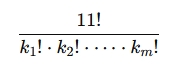
Takže vypočítajme teraz počet možností pre rozostavenie 4 – 4 – 2:

Čo myslíte, bude tých možností viac alebo menej ako v prípade, že sme nezaraďovali jednotlivých hráčov na ich pozície v danom systéme? Keď vynásobíme jednotlivé členy medzi sebou dostaneme výsledok, že počet možných usporiadaní hráčov vo futbalovom rozostavení 4-4-2 je tak isto 39 916 800. Tento počet zodpovedá permutáciám a kombináciám, ktoré sú popísané vyššie. Ak by ste skúsili vypočítať počet možných usporiadaní pre iný systém podľa vyššie uvedeného postupu zistíte, že pre úplné rozmiestnenie 11 hráčov je tento postup univerzálny bez ohľadu na konkrétne rozostavenie, pretože všetky pozície sú plne obsadené. Táto univerzálnosť postupu znamená, že výpočet pokrýva všetky možné permutácie bez ohľadu na rozostavenie, pokiaľ všetky pozície sú obsadené.