Štrngnime si

Predstav si, že by si mal narodeniny a pozval by si si na ich oslavu najlepších kamarátov a kamarátky. Spolu s tebou by sa na oslave zúčastnilo 10 osôb. Pripravil by si chlebíčky, zákusky a na prípitok vychladené detské šampanské. Po blahoželaniach hostí a odovzdaní prinesených darčekov by prišiel na rad prípitok šampanským. Samozrejme, neobišlo by sa to bez štrngania plnými pohárikmi.

A práve tu začína moja dnešná matematická úloha, ktorá vyvrcholí odhalením dôležitého vzťahu spätého s menom významného matematika. Moja otázka znie: koľko štrngnutí pri prípitku svojej narodeninovej oslavy by si počul?

Začnime vstupnými dátami. Na oslave sa zúčastňuje 10 osôb (ty a 9 hostí), očíslujme si ich číslami od 1 do 10. Každý si môže štrngnúť so všetkými ďalšími, ale nemôže si štrngnúť sám so sebou. To znamená, že každý si štrngne s 9 ďalšími osobami, napríklad 1 s 2, 3, atď., 2 s 1, 3, 4 atď., potom 3 s 1, 2, 4 atď. Všimni si, že 1 si štrngá s 2, ale aj 2 s 1. Treba si však uvedomiť, že toto štrngnutie neznamená započítať 2 štrngnutia, ale len 1 štrngnutie.

Uvedený stav si môžeme zobraziť v tabuľke. Vo vrchnom riadku a prvom stĺpci sú čísla reprezentujúce počet osôb. V poslednom stĺpci sú súčty akceptovaných štrngnutí jednotlivých osôb. Zelený krúžok značí štrngnutie, ktoré považujeme za akceptované a započítateľné, červený krížik značí nemožnosť štrngnutia sám so sebou a modrý krúžok znamená duálne štrngnutie dvoch osôb, z ktorých je však započítané len jedno.

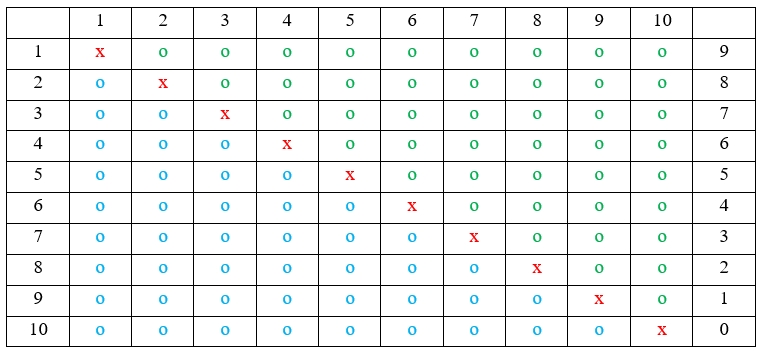
Teraz už stačí spočítať čísla v poslednom stĺpci a máme výsledok našej matematickej úlohy — počas narodeninového prípitku si si mohol vypočuť 45 štrngnutí.

V poslednom stĺpci sú zoradené čísla od 0 po 9. Ide o aritmetickú postupnosť, ktorá je, zjednodušene, definovaná ako postupnosť členov, pričom každý ďalší člen má rovnakú diferenciu d. V našom prípade je d=1 a každý jej člen je zväčšený presne o túto diferenciu.

S aritmetickými postupnosťami sa zaoberal aj slávny nemecký astronóm, matematik a fyzik Carl Friedrich Gauss. Raz dostal za úlohu spočítať prvých 100 prirodzených čísel 1 + 2 + 3 + … + 98 + 99 + 100. Všimol si, že súčet dvojíc čísel prvé s posledným, druhé s predposledným, tretie s tretím od konca atď. je vždy 101. Takýchto dvojíc je 50. Stačilo mu teda vynásobiť 101 x 50 a dostal výsledok 5 050. Jeho postup viedol k odvodeniu matematického vzorca pre súčet prvých n členov aritmetickej postupnosti s_n = n/2 * (a₁ + a_n), kde a₁ je prvý člen aritmetickej postupnosti, a_n je posledný člen aritmetickej postupnosti a n je počet členov aritmetickej postupnosti.

A ako by asi riešil náš štrngací matematický príklad sám Gauss?

1. 0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 9 + 9 + 9+ 9+ 9 = 45
2. Počet členov aritmetickej postupnosti n=10, a₁ = 0, a_n = 9. S_n = 10/2 * (0 + 9) = 5 * 9 = 45.

Je zrejmé, že pri malom počte členov aritmetickej postupnosti nie je problém vypočítať súčet aj manuálne a to pomerne rýchlo. Pri väčšom počte však použitie uvedeného matematického vzorca výpočty výrazne uľahčuje a zrýchľuje.